Pisanie skryptów w środowisku Mechanical nie musi ograniczać się do prostej automatyzacji czynności niezbędnych do wykonania analizy MES. Dzięki narzędziom takim jak np. ResultReader możemy uzyskać dostęp do surowych wyników w pliku RST i przetworzyć wyniki w sposób specyficzny dla naszych potrzeb, co zwykle wymaga implementacji szeregu funkcji matematycznych. Niniejszy artykuł przybliży dwa zaimplementowane w Mechanical API obiekty, których wykorzystanie pozwoli zaoszczędzić nieco czasu: Vector3D i Matrix4D.
Z uwagi na zakres zagadnienia, artykuł został podzielony na 3 części, z których każda porusza kolejny etap pracy:
Część I – Obiekty Vector3D i Matrix4D: zawiera krótkie wprowadzenie do programowania obiektowego – jak je tworzyć i jak z nich korzystać.
Część II – Transformacja koordynat do lokalnego układu współrzędnych
Część III – Odczyt danych z pliku RST i transformacja tensora naprężeń: opisuje proces odczytu danych z pliku RST (na bazie elementów powłokowych) oraz ich transformacji do lokalnego układu współrzędnych z wykorzystaniem obiektów Vector3D i Matrix4D.
Transformacja koordynat do lokalnego układu współrzędnych
Pełen opis przykładu kodu transformującego koordynaty punktu 3D do lokalnego układu współrzędnych z wykorzystaniem opisanych wcześniej obiektów Vector3D i Matrix4D.
Wstęp
W ramach praktycznego przykładu, przygotujemy metodę transformującą koordynaty punktu pomiędzy globalnym a lokalnym układem współrzędnych. Transformacja koordynat wymaga wykonania dwóch operacji:
- Znalezienia wektora pomiędzy początkiem lokalnego CS a rozpatrywanym punktem.
- Transformacji koordynat uwzględniającej lokalne kierunki osi X/Y/Z.
- Dodatkowa transformacja koordynat, jeśli układ lokalny jest cylindryczny.
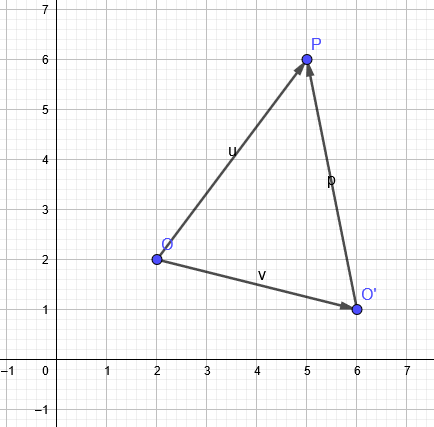
Jeśli początek globalnego układu współrzędnych oznaczymy jako O, a punkt w przestrzeni jako P, to wektor OP (u) o koordynatach xyz definiuje nam położenie punktu P w globalnym układzie. W praktyce, wektor ten definiujemy za pomocą koordynat xyz.
| u = Vector3D(x,y,z) |
Jeśli początek lokalnego układu współrzędnych oznaczymy jako O’, to wektor OO’ (v) definiuje nam jego położenie względem początku układu globalnego. W praktyce, wykorzystujemy własność Origin obiektu drzewa Coordinate System. Własność Origin to lista trzech koordynat, a wektor definiujemy za pomocą trzech parametrów. Dla zmniejszenia ilości kodu, wykorzystamy symbol * rozbijający listę na osobne parametry:
| local_cs = DataModel.GetObjectsByName(local_cs_name)[0] v = Vector3D(*local_cs.Origin) |
Koordynaty punktu P w lokalnym układzie współrzędnym to nic innego jak spojrzenie na punkt P z perspektywy punktu O’. Wykorzystując nasze wektory, O’P możemy wyliczyć poprzez różnicę wektorową OP (u) i OO’ (v). Obiekt Vector3D implementuje operatory matematyczne, dlatego różnicę wektorową możemy zapisać w postaci:
| p = u – v |
W przypadku, kiedy osie układów są identyczne, możemy zakończyć transformacje i zwrócić wyznaczony wektor jako koordynaty punktu P w lokalnym układzie współrzędnych.
Macierz obrotu (Rotation Matrix)
W przypadku, kiedy nasz układ lokalny jest obrócony, musimy wykonać dodatkowe transformacje układu, aby nasze koordynaty miały odpowiednie znaki oraz wartości. Dysponując macierzą obrotu Q, cała operacja sprowadza się do operacji mnożenia naszego wektora p przez macierz Q. W teorii, znalezienie macierzy obrotu Q wymaga znalezienia 3 obrotów euklidesowych niezbędnych do przejścia z układu globalnego do lokalnego. Operacja nie należy do najprostszych i wymaga kilku założeń (ścieżek postępowania) oraz operacji na macierzach. Zainteresowanych zapraszam do bliższego zapoznania się z zagadnieniem: macierz obrotu i kąty Eulera.
W publikacjach tych nie znajdziemy jednej interesującej informacji na temat definicji macierzy obrotu, która jest niezmiernie ważna z punktu widzenia informacji w naszym posiadaniu (w naszym, czyli skryptujących użytkowników Mechanical API).
Otóż macierz obrotu Q możemy zdefiniować za pomocą wektorów kierunkowych lokalnego układu współrzędnych. Jeśli osie lokalnego układu współrzędnych są zdefiniowane poprzez wektory X’/Y’/Z’, to macierz obrotu Q dla tego układu możemy zapisać jako:
Jeśli przyjrzymy się uważnie własnością lokalnego układu współrzędnych w Mechanical, to zauważymy tam pozycję Directional Vectors.
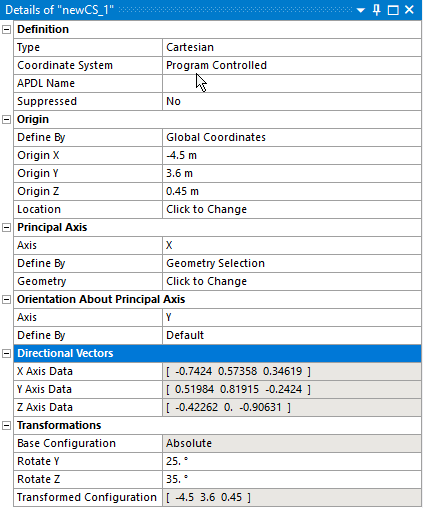
Z poziomu API, dla obiektu Coordinate System wektory te znajdziemy pod nazwami XAxis, YAxis oraz ZAxis. Obiekt Matrix4D posiada statyczny konstruktor, który pozwala na definicję macierzy kolumnami. Możemy wykorzystać ten konstruktor oraz lokalne wektory kierunkowe, a następnie transponować utworzoną macierz. Należy pamiętać o następujących rzeczach:
- Wektory kierunkowe mają postać list liczb zmiennoprzecinkowych, dlatego uprzednio należy utworzyć obiekty Vector3D;
- metoda Transpose wykonuje operację na obiekcie i nie zwraca wartości (void).
Jeśli zmienna local_cs zawiera referencję do lokalnego układu współrzędnych w drzewku analizy (Outline), nasz kod będzie wyglądał następująco:
| Q = Matrix4D.CreateSystem( Vector3D(*local_cs.XAxis), Vector3D(*local_cs.YAxis), Vector3D(*local_cs.ZAxis) ) Q.Transpose() |
Od wyniku dzieli nas jedynie operacja mnożenia wektora przez macierz. Niestety, API nie implementuje operatora, który pozwoli na zapis p * Q. Obiekt Matrix4D posiada natomiast metodę Transform(Vector3D), która wykonuje tę operację.
| pp = Q.Transform(p) |
Rodzaj układu współrzędnych
Jeśli lokalny układ współrzędnych jest kartezjański, dalsze operacje nie są wymagane. Jeśli użytkownik wybrał układ cylindryczny, czeka nas jeszcze transformacja koordynat X i Y.
Wyznaczenie lokalnego X to nic innego jak wartość projekcji wektora 3D na płaszczyznę XY:
| (pp.X**2. + pp.Y**2)**0.5 |
W przypadku kąta Theta, zależy nam na wyniku w zakresie -π/π, dlatego wykorzystamy funkcję math.atan2.
| math.degrees(math.atan2(pp.Y, pp.X) |
Porządkując skrawki kodu zaprezentowane powyżej, możemy utworzyć funkcję, która jako argumenty przyjmuje x, y, z punktu oraz nazwę lokalnego układu współrzędnych.
Finalny kod
def Transform_CS(x, y, z, local_cs_name): import math local_cs = DataModel.GetObjectsByName(local_cs_name)[0] u = Vector3D(x, y, z) v = Vector3D(*local_cs.Origin) Q = Matrix4D.CreateSystem( Vector3D(*local_cs.XAxis), Vector3D(*local_cs.YAxis), Vector3D(*local_cs.ZAxis) ) Q.Transpose() p = Q.Transform(u-v) if local_cs.CoordinateSystemType == CoordinateSystemTypeEnum.Cartesian: return (p.X,p.Y,p.Z) elif local_cs.CoordinateSystemType == CoordinateSystemTypeEnum.Cylindrical: return ( (p.X**2.+p.Y**2.)**0.5, math.degrees(math.atan2(p.Y, p.X)), p.Z ) |
Autor: Bartosz Płochocki, MESco sp. z o.o.
Zainteresował Cię temat? Zobacz nasze szkolenia poświęcone skryptowaniu na poziomie podstawowym i zaawansowanym.
