Piłka baseballowa, piłka nożna, kierowane pociski rakietowe oraz wirniko-żagle na statkach – co je łączy? Otóż na wszystkie te przedmioty w trakcie ruchu działa tajemnicza siła. Odpowiedzią na pytanie co to za siła zajęło się grono naukowców i badaczy, którzy na przestrzeni lat starali się opisać efekty zmiany kierunku np. lotu piłek tenisowych, kul muszkietowych i armatnich. Z tego grona szczególnie wyróżnia się Heinrich Magnus – niemiecki fizyk, który opisał zjawisko, będące odpowiedzią na pytanie powyżej. Jednak ludzkość potrzebowała jeszcze stu trzech lat żeby poznać przyczynę tego zjawiska – dopiero w 1955 E. Krahn połączył ze sobą lepkość, warstwę przyścienną oraz efekt Magnusa.
No to co to jest, ten Efekt Magnusa
Tak nazywa się zjawisko polegające na powstaniu siły prostopadłej do kierunku przepływu, działającej na obracającą się i poruszającą się względem płynu bryłę obrotową. Brzmi skomplikowanie? Ułatwimy to. Przenieśmy ten trójwymiarowy problem na płaszczyznę 2D.
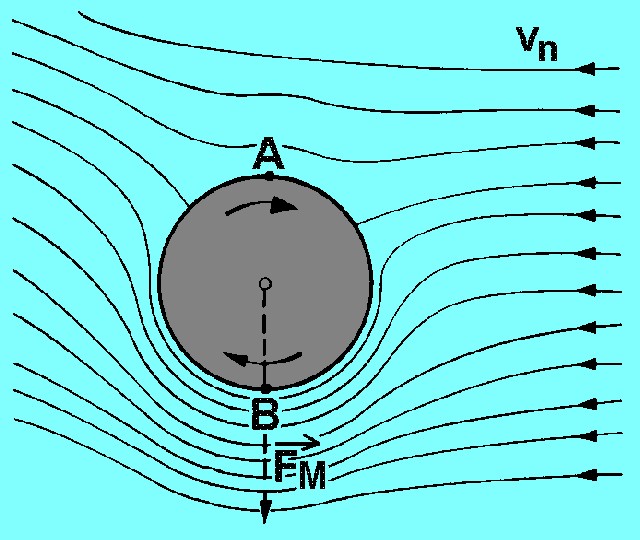
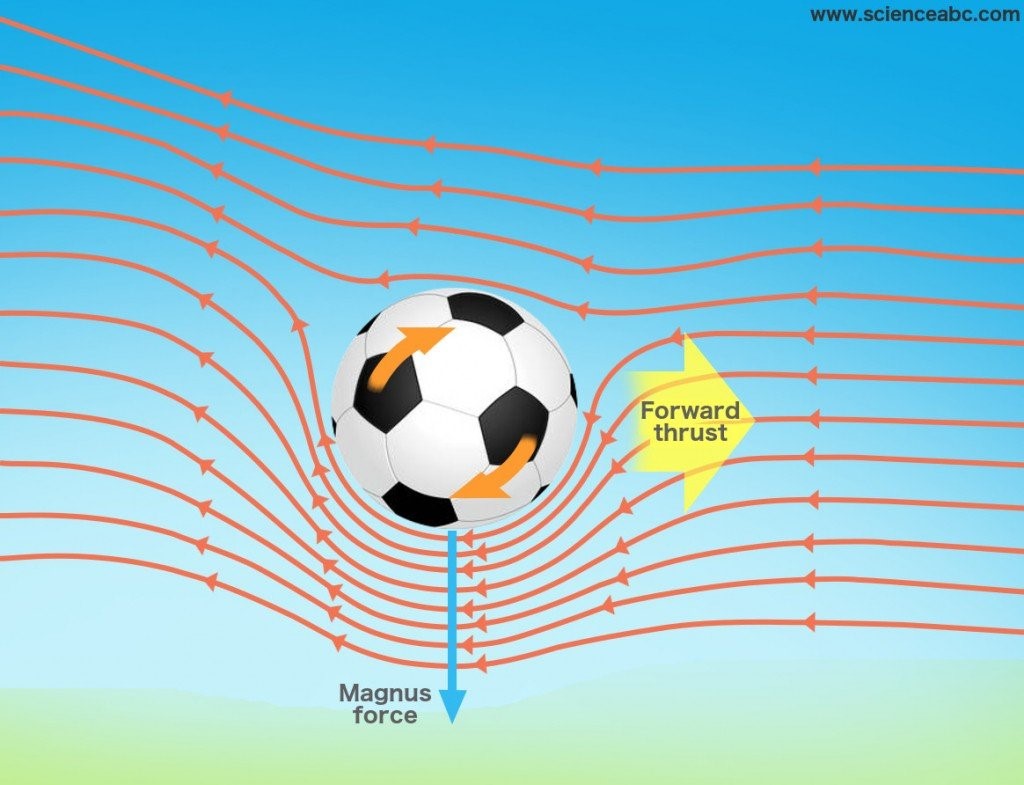
Mamy więc koło obracające się wokół własnej osi w stronę przeciwną do wskazówek zegara oraz płyn poruszający się z pewną prędkością i nacierający na kulkę od prawej strony. Struga płynu musi rozdzielić się na dwie by ominąć kulkę. I tu zaczyna się magia. Część strugi przepływająca koło punktu B zostaje przyspieszona, a jej tor ruchu zakrzywiony z powodu obracającej się kulki. Tymczasem struga opływająca punkt A zostanie spowolniona z tego samego powodu, co dodatkowo prowadzi to powstawania zawirowań. Tworzą się dwa obszary: w punkcie A z płynem przepływającym z niską prędkością oraz w punkcie B z płynem przepływającym w wysoką wartością prędkości. Z równania Bernoulli’ego wynika , że w miejscach wysokiej wartości prędkości płynu, następuje spadek jego ciśnienia (punkt B) i na odwrót jest w punkcie A – jest to obszar wysokiego ciśnienia płynu. Różnica tych ciśnień powoduje powstanie siły skierowanej prostopadle do ruchu płynu, nazywanej siłą Magnusa (w naszym przypadku wektor tej siły skierowany jest na „dół”), ale zwrot tej siły zależy od kierunku przepływu płynu oraz rotacji bryły (czyli zależy od tego czy „kręci się” zgodnie czy przeciwnie ze wskazówkami zegara). W ten oto sposób powstaje siła powodująca rotację w locie piłki. Dobrze obrazuje to krótki filmik poniżej:

Było projektowane, modelowane i liczone – teraz czas się pochwalić wynikami!
Na początek małe porównanie między taką sytuacją w której zachodzi efekt Magnusa (kulka/cylinder się obraca), a taką gdy prędkość obrotowa bryły wynosi 0 [rad/s] i wspomniany wyżej efekt nie zachodzi.
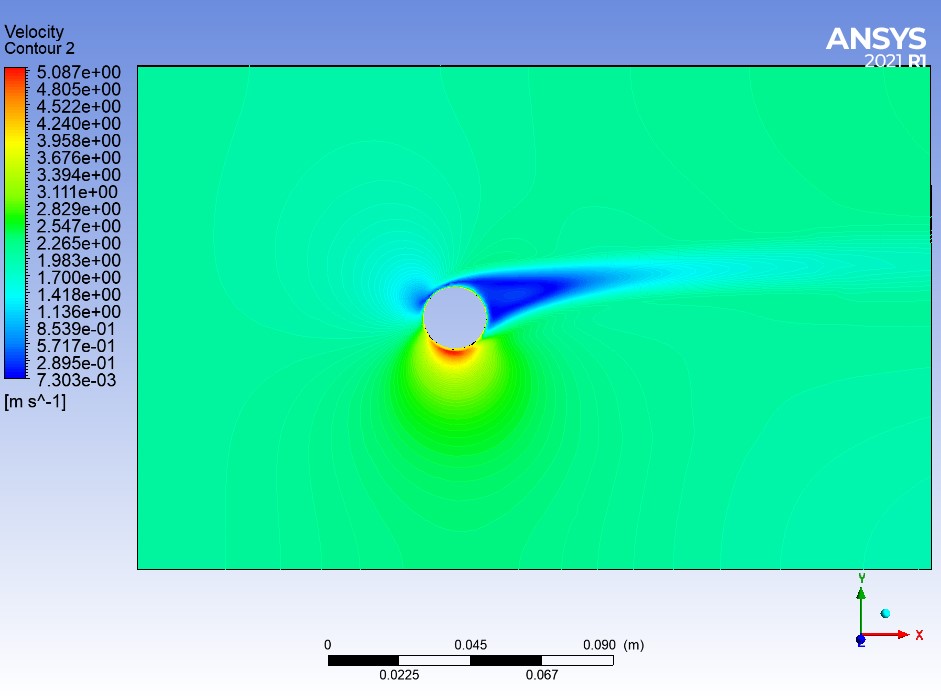
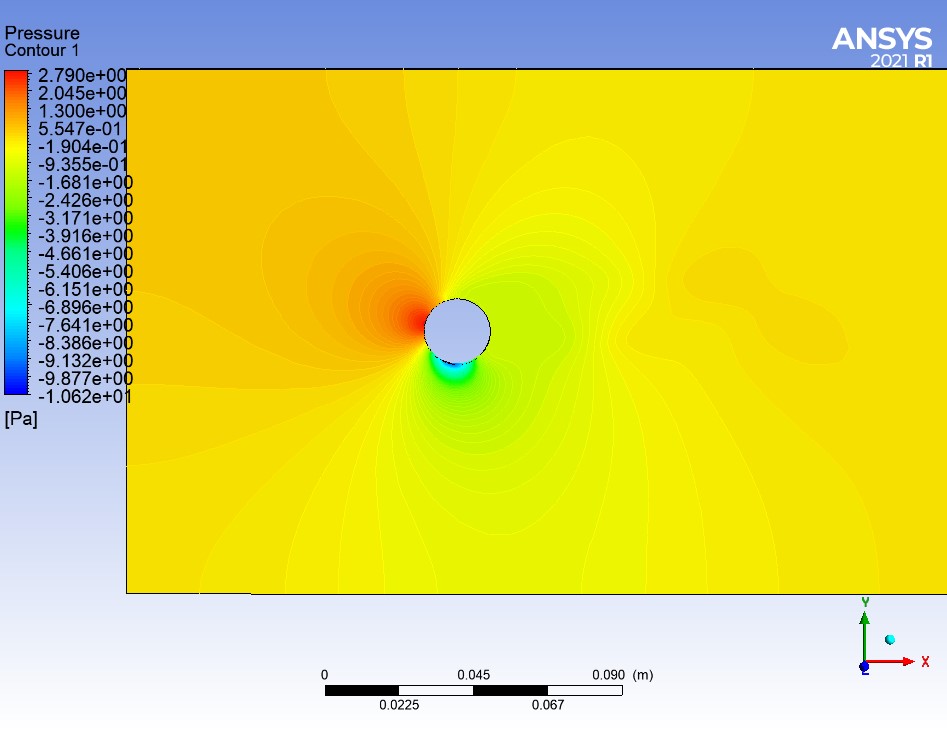
Na Rysunku 2 przestawiono kontur prędkości płynu w domenie dla prędkości obrotowej ω = 400 [rad/s]. Widać odchylenie strugi płynu. Obszar na „dole” kulki (kolor czerwony) jest tym w którym powietrze porusza się szybciej, przez co następuje tam spadek ciśnienia. Analogicznie obszar na „górze” (kolor niebieski) jest obszarem płynu o małej prędkości i wysokim ciśnieniu. Siła Magnusa zaczepiona jest w środku kuli i skierowana prostopadle w dół.
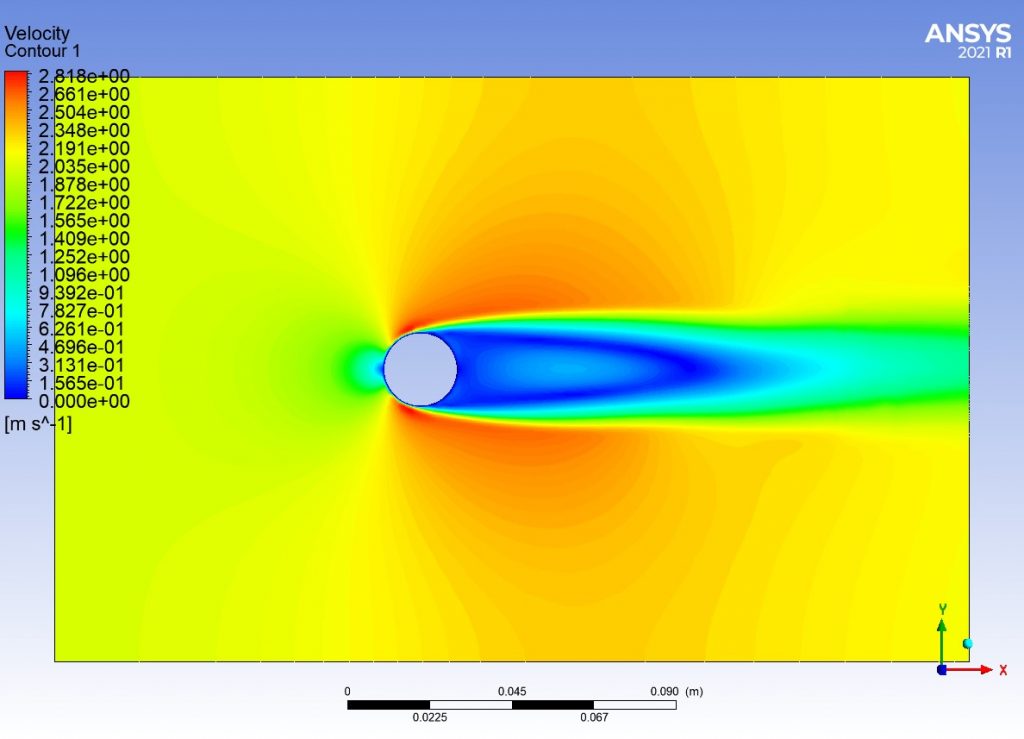
Na Rysunku 3 przestawiono kontur prędkości płynu w domenie dla prędkości obrotowej ω = 0 [rad/s]. Ze względu na zerową prędkość obrotową kulki nie ma widocznych żadnych odchyleń prędkości – jest to zwykły przypadek opływu kuli przez płyn.
Następnie dla stałej prędkości przepływu równej v = 2 [m/s] przeprowadzono obliczenia dla 3 kolejnych prędkości obrotowych kuli (krok co 200 [rad/s]). Porównanie wyników znajduje się poniżej.
Dodatkowym parametrem były pomiary siły Magnusa działającej na kulkę. Siła ta była mierzona przez cały czas trwania symulacji. Na poniższym wykresie dobrze widać duże zmiany na początku obliczeń jednak po około 0,2 [s] wartość siły Magnusa stabilizuje się i układ jest w równowadze. Wykres stworzono dla parametrów: v = 2 [m/s] oraz ω = 500 [rad/s]

| ω [rad/s] | Fy [N] |
| 200 | -0,084 |
| 300 | -0,148 |
| 400 | -0,21 |
| 500 | -0,30 |
| 600 | -0,36 |
Poniżej kilkusekundowa animacja przedstawiająca tworzenie się efektu Magnusa dla danych wartości przepływu: v = 2 [m/s] oraz ω = 400 [rad/s]:

Jak już było wspomniane wcześniej efekt Magnusa ma ogromne znaczenie we wszelkich sportach, w których korzysta się z piłki, przede wszystkim w piłce nożnej, golfie, baseballu, siatkówce i koszykówce. Dodatkowo brać go pod uwagę muszą balistycy przy obliczaniu trajektorii lotu pocisków. Dodatkowa różnica wynika z faktu, że piłka oprócz rotacji ma również pewną prędkość początkową.
No fajnie wiedzieć, ale korzysta się chociaż z tego?
Jak już było wspomniane wcześniej efekt Magnusa ma ogromne znaczenie we wszelkich sportach, w których korzysta się z piłki, przede wszystkim w piłce nożnej, golfie, baseballu, siatkówce i koszykówce (pojedynki rewolwerowe też… ale to nie sport). Dodatkowo brać go pod uwagę muszą balistycy przy obliczaniu trajektorii lotu pocisków rakietowych i programowaniu systemów sterowania rakietami samonaprowadzającymi.
Co zaś tyczy się zastosowań w przemyśle, zjawisko to wykorzystuje się w branży transportowej. Rotor Flettnera jest gładkim walcem (cylindrem) umiejscowionym w miejscu masztu, którego prędkością obrotową można sterować. Statek może być wyposażony w jeden duży lub kilka mniejszych rotorów Flettnera i mogą one stanowić zarówno główny układ napędowy jak i pomocniczy, wykorzystując siłę wiatru i prędkość obrotową cylindrów do wytworzenia siły ciągu. Poniżej przedstawiono kilka współczesnych okrętów posiadających rotor Flettnera jako jednostkę napędu pomocniczego.
Natomiast pierwszy taki okręt zadebiutował w 1924 roku:

Co ciekawe wirnik Flettnera zamontowany pod linią wodną statku umieszczony poziomo z boku kadłuba, pełni rolę stabilizatora okrętu na wzburzonym morzu. To rzadkie rozwiązanie stosuje się w większych jachtach motorowych i innych jednostkach morskich.
Próbowano również zastosować rotor Flettnera w lotnictwie. Ponieważ pokazany powyżej statek wzbudził spore zainteresowanie, przeprowadzono badania w tunelu aerodynamicznym i uzyskano zaskakujące wartości siły nośnej, kilkukrotnie większe od tych uzyskanych z analogicznej powierzchni skrzydeł. Wykonano kilka prototypów, ale ostatecznie napęd ten okazał się niewystarczająco wydajny, a wirniki powodowały powstawanie dużych oporów powietrza. Czasem jedynie modele samolotów posiadają ten rodzaj napędu. Poniżej zdjęcie prototypu z lat 30. XX wieku.

Świat ewidentnie czeka na kolejnego wynalazcę który będzie umiał zastosować Efekt Magnusa w przemyśle. Szczególnie, że teraz inżynierowie mają do dyspozycji potężne narzędzia w postaci symulacji komputerowej. Możemy więc zbudować wirtualny model i badać wpływ wielu różnych parametrów na zachowanie się produktu… Mnie to ciekawi.
FYI: Wszystkie obliczenia zostały przeprowadzone w ANSYS FLUENT.
Autor: Bartosz Stężowski, Akademia Górniczo-Hutnicza