Jedną z cech bycia inżynierem jest to, że czasem zwyczajne rzeczy mogą zaintrygować i zająć myśli na wiele godzin. Jako inżynier zajmujący się zagadnieniami przepływowymi, na co dzień mierzę się z problemami o raczej dużej skali: absorberami energetycznymi, kanałami spalin, opływami budynków itp. Jednak często największą satysfakcję, sprawia przełożenie wiedzy i intuicji inżynierskiej pozyskanej w pracy zawodowej na rzeczy, które otaczają nas w codziennym życiu.
W poniższym artykule chciałbym pokazać, jak wygląda klasyczne dojście do sedna problemu przepływowego na bardziej przyziemnym przykładzie.
Załóżmy następującą sytuację: do niewielkiego pojemnika z wodą wkładamy blender tak, aby głowica stykała się z dnem, i uruchamiamy go. Następnie podnosimy blender do góry – pojemnik z wodą podniesie się razem z blenderem.
 |  |
Efekt „zassania” blendera można też poczuć, gdy uruchomimy blender niewiele ponad dnem – natychmiast głowica zostanie pociągnięta do dna.
Oczywiście dla części z czytających, szczególnie dla poruszających się na co dzień w świecie przepływów ten efekt nie będzie wielką tajemnicą, ale dla celów narracyjnych uznajmy, że takie zachowanie jest dla nas zagwozdką 🙂
To, co większość inżynierów i naukowców potwierdzi to to, że aby dobrze zrozumieć i/lub odwzorować pewne zjawisko warto zacząć od maksymalnego uproszczenia zagadnienia. Po tym, jak już dobrze poznamy układ prosty, komplikujemy zadanie dodając kolejne elementy układanki. Ta sama zasada przekłada się również na prace z modelami numerycznymi. Przykład z blenderem może być dość skomplikowany do opisania, szczególnie gdy nie znamy dokładnie końcowego efektu. Mamy tutaj do czynienia ze zjawiskiem dość burzliwym i niestacjonarnym – szybkim ruchem ostrza powodującym ruch wirowy płynu czy skomplikowaną geometrią głowicy. Dlatego spróbujmy ten sam efekt uzyskać na prostszym układzie.
Przyjmijmy, że dwie płyty, zrobione z lekkiego materiału (np. styropianu) zetkniemy ze sobą dłuższymi krawędziami. Dodatkowo w jednej z nich wytniemy otwór na środku i do otworu doprowadzimy strumień powietrza (np. suszarką do włosów).
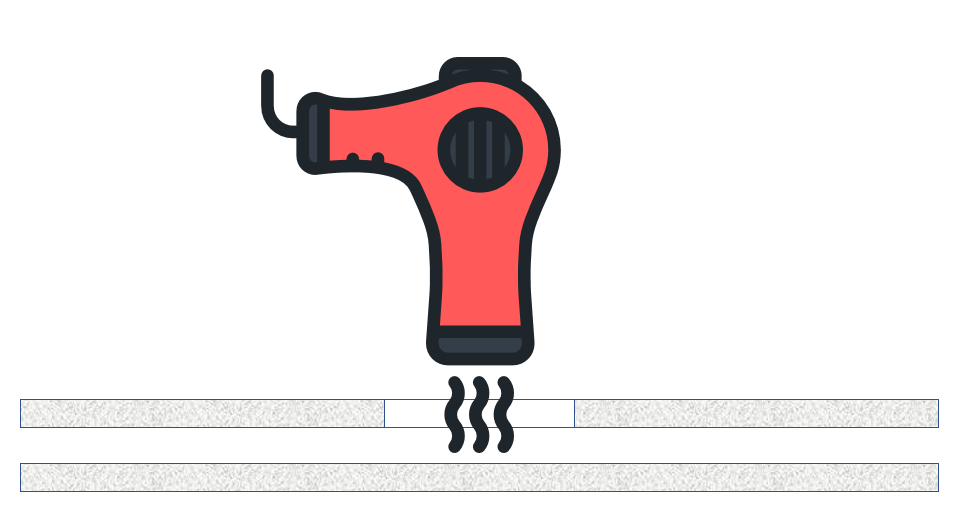
Intuicja podpowiada, że dolna płyta, jeśli nie będzie podparta, spadnie w kierunku działania przyspieszenia ziemskiego. Jednak okazuje się, że przy odpowiednich warunkach (waga i wielkość płyt, moc suszarki) można uzyskać stabilny układ gdzie dolna płyta „przylepi się” do górnej.

Spróbujemy odwzorować ten efekt w modelu numerycznym CFD. Zgodnie z tym co napisano wcześniej, stworzymy maksymalnie uproszczony model, a następnie postaramy się go udoskonalić w kolejnych iteracjach modelu.
Jednym z najczęstszym uproszczeniem, a jednocześnie bardzo użytecznym, jest redukcja wymiarów modelu do 2D. Zastosujemy model osiowo symetryczny. Nie będziemy również symulowali ruchomej dolnej płyty, zamiast tego przeliczymy kilka wysokości szczeliny h i sprawdzimy jaką siłę otrzymamy na powierzchni dolnej płyty.
Oczywiście symulacja z dynamiczną siatką jest możliwa, jednak nie ma potrzeby komplikować zadania o ile cel symulacji zostanie spełniony. Do prostych obliczeń w zupełności wystarczy nam bilans sił, a dzięki rezygnacji z ruchomej siatki będziemy mogli wykonać obliczenia w stanie ustalonym.
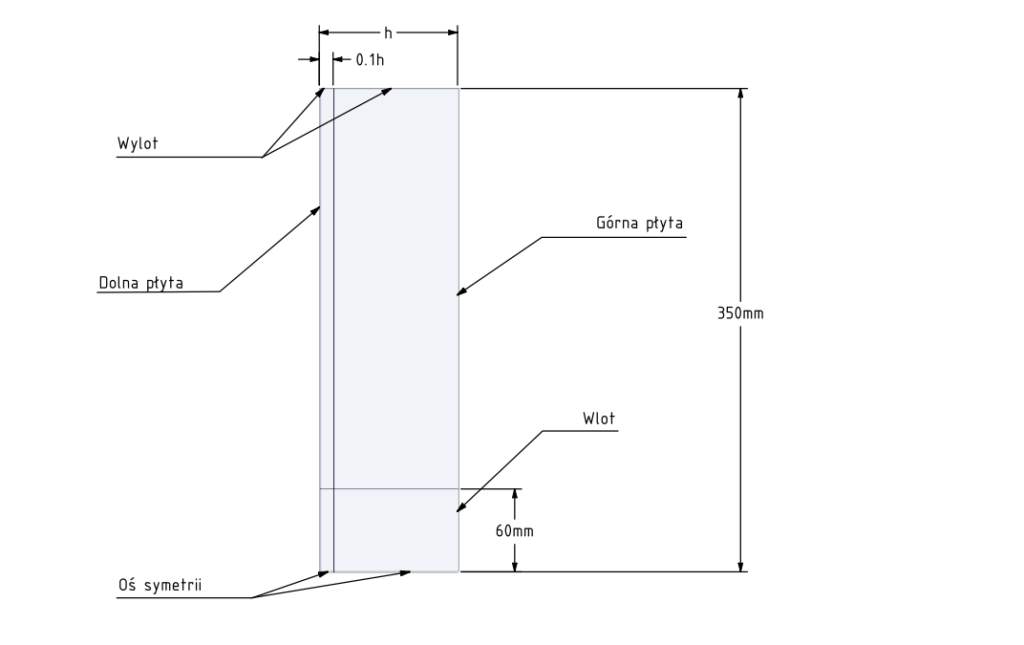
Geometria składa się z 4 powierzchni, połączonych wspólną topologią. W ten sposób bardzo łatwo jest utworzyć siatkę strukturalną oraz kontrolować rozmiar i rozkład elementów. Użytkownik może za pomocą funkcji Face Meshing wymusić strukturalne rozmieszczenie elementów, przy założeniu że powierzchnia posiada 4 krawędzie zewnętrzne. W takiej sytuacji rozłożenie elementów można kontrolować przez zadawanie lokalnego zagęszczenia na krawędziach.
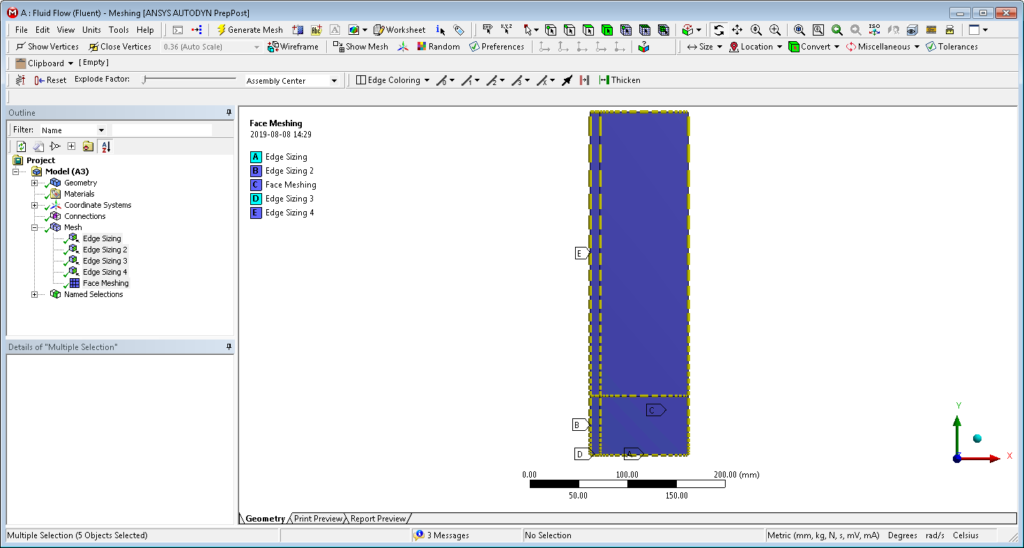
W symulacjach, gdzie efekty przyścienne są ważne z punktu widzenia celu symulacji korzystnie jest nie stosować modeli turbulencji korzystających z funkcji przyściennych. Dlatego w naszych rozważaniach użyjemy modelu k-omega SST. Nie można jednak zapominać, że aby taka symulacja miała sens, siatka musi być odpowiednio przygotowana. Jednym z najczęściej używanych parametrów do oceny siatki pod kątem modelu turbulencji (ale często nie jedynym!) jest y+, czyli bezwymiarowa odległość pierwszego elementu od ściany. Z tego powodu przy symulowaniu zjawiska będziemy kontrolować wartość y+ dla poszczególnych przeliczeń. Dzięki zastosowanemu podziałowi geometrii na 4 obszaru, możemy w razie potrzeby zagęścić siatkę przy ścianie.
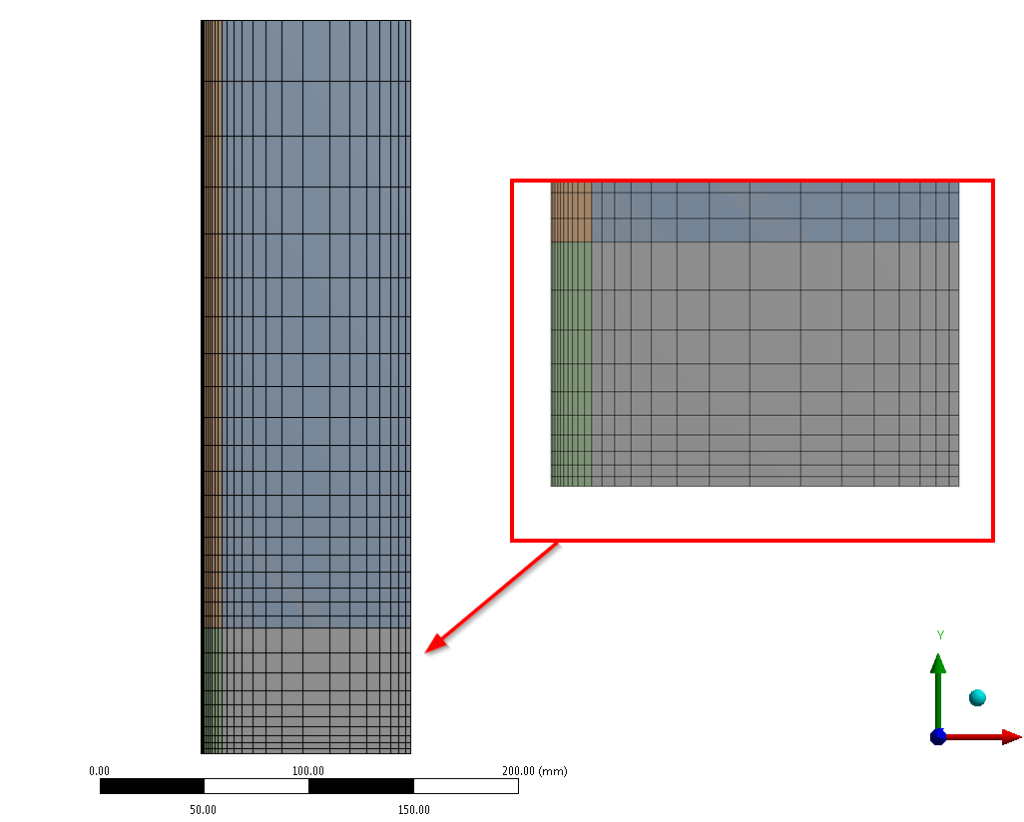
Dla uproszczenia, na początek założymy stałą wartość prędkości na wlocie na poziomie 1 m/s. Pierwsze przeliczenie wykonano dla wysokości h = 100 mm.
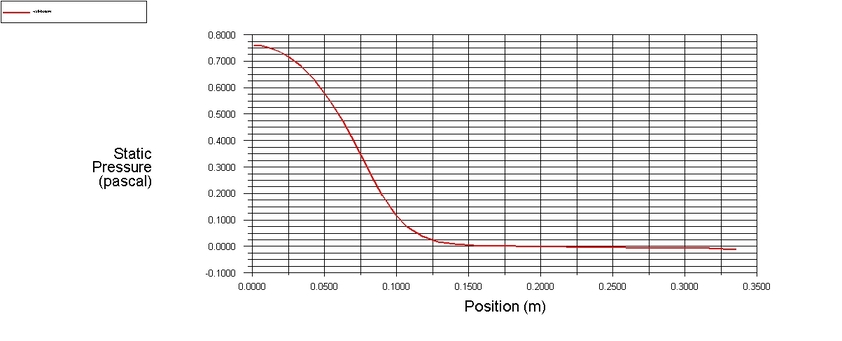
Rozkład ciśnienia na dolnej powierzchni pokazuje, że w centralnej części płyty występuje wysoka siła działająca zgodnie z kierunkiem przepływu, czyli dopychającą płytę w dół. Zwrócić należy jednak uwagę że im dalej od punktu centralnego tym ciśnienie bardziej spada, a wręcz w pewnym punkcie zmienia znak na ujemy. W tym konkretnym ustawieniu jest to jednak efekt pomijalnie mały. Po scałkowaniu ciśnienia po powierzchni otrzymamy siłę. Dla h = 100mm siła na dolnej płycie wyniosła 0.013 N.

Na rozkładzie prędkości płynu wyraźnie widać obszar niskiej prędkości po środku płyty, tzw. punkt stagnacji, gdzie ciśnienie statyczne gwałtownie rośnie. Maksymalny y+ wyniósł ok. 1.8 co jest przyzwoitym wynikiem, ale w kolejnych iteracjach postaramy się go jeszcze poprawić.
W kolejnym kroku, model sparametryzowano tak, że parametrem wejściowym do analizy była wysokość szczeliny, a wyjściowym siła na dolnej powierzchni. Dodatkowo mierzono maksymalny y+ oraz ciśnienie na wlocie (straty przepływu). Przeliczono 12 Design Pointów, każdy z różną wysokością szczeliny (h1) od 100 do 1 mm.
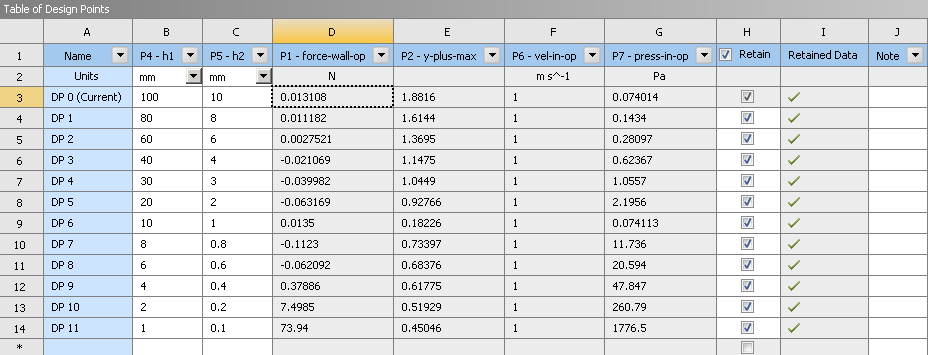
Wyraźnie widać, że niektóre punkty wykazały wartość ujemną, co oznacza że sumarycznie struga będzie podciągać płytę do góry. Ponadto widać, że punkt 10 odstaje nieco od reszty punktów.
Dowiedzmy się zatem, skąd wynika negatywna wartości siły. Porównamy rozkład ciśnienia na powierzchni dolnej płyty dla wysokości szczeliny 6mm (który uzyskał najniższą wartość siły), oraz dla 100mm.
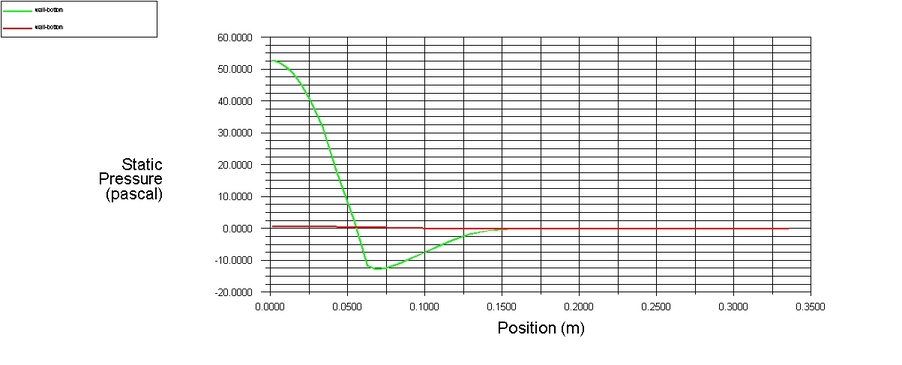
To czego na pewno się spodziewamy to to, że w punkcie centralnym płyty zauważymy dużo wyższe ciśnienia statyczne. Znacznie większą siłą zadziałamy na obiekt na który dmuchamy z bliska niż na ten który jest od nas dużo dalej. Jednak ciekawsze jest to, co zobaczymy za obszarem obejmującym punkt stagnacji. Przy mniejszej szczelinie ciśnienie osiąga wartości ujemne i to w znacznym obszarze – od ok 0.06m do 0.15m.
Zastanawiające jest też to, że mimo iż wartość podciśnienia jest mniejsza niż w ekstremum nadciśnienia, i pole powierzchni pod wykresem będzie najprawdopodobniej większe niż w podciśnieniu po scałkowaniu otrzymamy wartość ujemną. Jak to jest możliwe?
Pamiętajmy, że rozwiązujemy układ osiowo-symetryczny. A zatem im większa wartość Position na wykresie, tym większy promień, więc pole powierzchni rośnie w kwadracie a nie liniowo, jak sugeruje wykres.
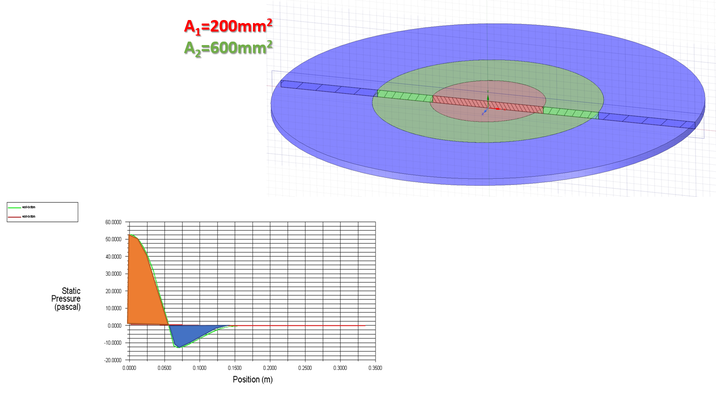
Z powyższego wykresu można wyciągnąć jeszcze jedną informację – płyta mogłaby być dużo mniejsza, gdyż za promieniem 0.15m ciśnienie właściwie wyrównuje się z 0 i tracimy efekt przyciągania.
Obszar niskiego ciśnienia tworzy się ze względu na bardzo duże przyspieszenie strugi za punktem stagnacji. Przez to, że na środku płyty leży punkt stagnacji, powietrze rozpływa się na boki. Z drugiej strony, szczelina ma niewielką wysokość, więc powietrze nie może odbić się do góry. Mówiąc prościej, jest tu na tyle mało miejsca że struga koncentruje się na dolnej powierzchni i przyspiesza, co oczywiście powoduje spadek ciśnienia statycznego. Efekt ten wyraźnie widać na rozkładzie prędkości.


Żeby uzyskać nieco dokładniejszy wynik przeliczono ten sam układ z dużo gęstsza siatką. Dodatkowo zwiększono ilość przeliczanych Design Pointów aby lepiej odwzorować charakterystykę układu.
Mimo iż siatka została zagęszczona, a y+ mocno zredukowany to charakterystyka układu nie zmieniła się znacząco. Poprawiony został punkt, który odstawał od charakterystyki, oraz otrzymaliśmy dużo większą rozdzielczość rozwiązania.
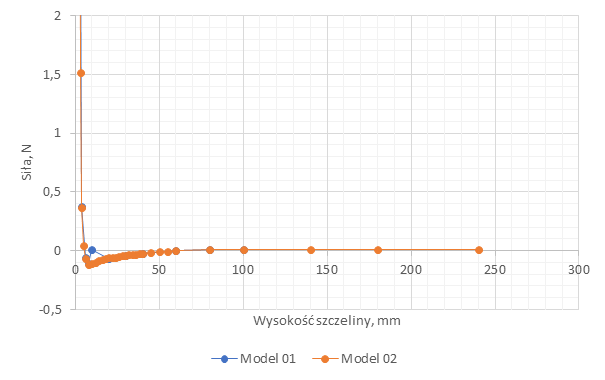
Co mówi nam ten wykres, w kontekście celu tej analizy? Otóż jeżeli waga płyty będzie odpowiednio mała, tj. nie więcej niż 11g (0.11N / 9.81 m/s2 = 0.011kg) i szczelina odpowiednio niewielka, tj. między 6 a 12 mm to siła generowana przez efekt dyszy będzie równoważyć siłę ciężkości płyty.
Trzeba zaznaczyć, że model ten posiada dość spore uproszczenie – stała prędkość przepływu na wlocie. W rzeczywistości, wszystkie urządzenia wymuszające przepływ działają z pewną charakterystyką. Zatem jeśli użyjemy do tego doświadczenia suszarki do włosów, przy małych wysokościach szczeliny będzie ona pracowała z dużo gorszą wydajnością. Przy niskich wartościach h1 zauważyć można nagły wzrost oporów przepływu – brzmi logicznie biorąc pod uwagę, że przedmuchujemy tą samą ilość powietrza dla szczeliny 1mm i 200mm.
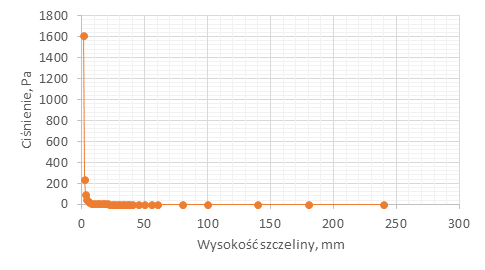
We Fluencie, możliwe jest zastosowanie warunku brzegowego oddającego charakterystykę urządzenia, tj. przepływ przez urządzenie w funkcji oporu przepływu generowanych przez zasilany układ. Zastosowano charakterystykę suszarki wg [1].
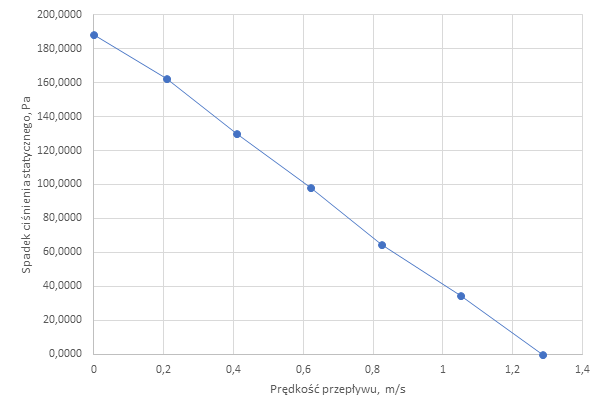
Co ciekawe, efekt podciągania płyty po zastosowaniu charakterystyki jeszcze się pogłębił. Być może dlatego że charakterystyka opisywała nieco mocniejszą suszarkę niż przyjęto na początek, a być może dlatego że warunek brzegowy naturalnie wypośrodkował przepływ do oporów kanału.

Ostatecznie, przyjmując parametry płyty, tj. grubość i gęstość materiału można oszacować, dla jakich wysokości szczeliny płyta nie będzie spadać.
Zakładając grubość płyty na poziomie 2mm i promieniu 35cm otrzymujemy objętość 0.00077 m3.
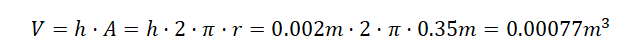
Przyjęto gęstość styropianu 20 kg/m3 co daje masę:

Siła ciężkości wynosi zatem:
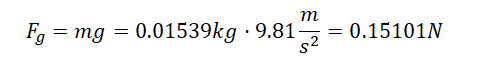
Do tego musimy jeszcze uwzględnić siłę wyporu. Będzie ona niewielka, ale w porównaniu do sił które uzyskujemy od strugi i siły ciężkości będzie to ważny element. Siła wyporu wynosi zatem:

Aby płyta zawisła w powietrzu siła generowana przez strugę Fa oraz siła wyporu Fw powinny zrównoważyć siłę ciężkości Fg:
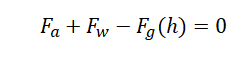
Na wykresie poniżej przedstawiono wartość tego wyrażenia w zależności od wysokości szczeliny. Widać na nim dwa punkty przecięcia wykresu z osią X. Sugeruje to, że w tych dwóch punktach układ uzyska stabilność.
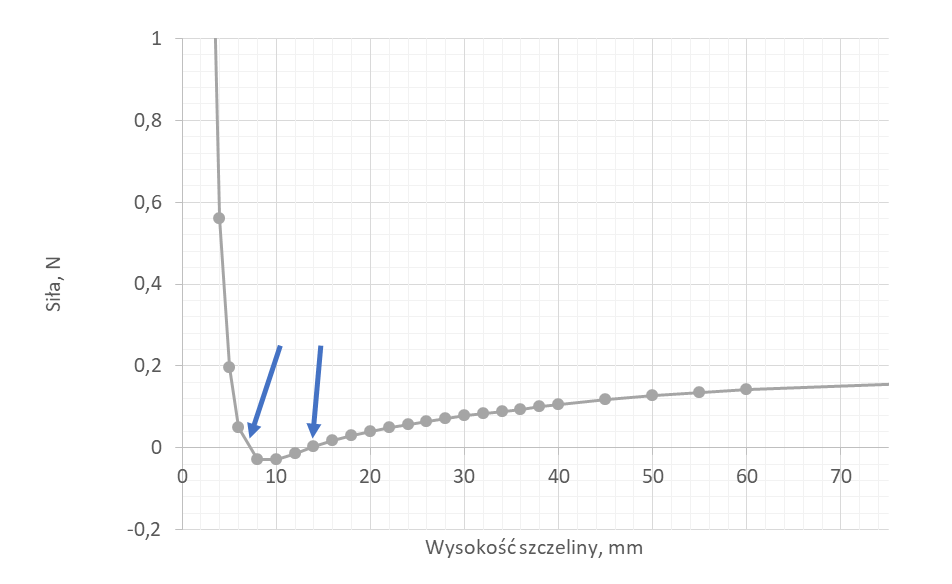
Udowodniliśmy ostatecznie, w oparciu o model numeryczny, że takie zjawisko może zachodzić w rzeczywistości. Wracając do pierwotnego przykładu – blendera efekt ten będzie zwielokrotniony gdyż prędkość przepływu wody będzie zapewne większa niż w pokazanym przykładzie, a dodatkowo większa gęstość płynu potęguje siły działające na ściany.
Jak widać nawet najprostsze zagadnienie, jeśli rozłożyć je na czynniki pierwsze, może być intrygujące i posiadać wiele ciekawych aspektów. Taką samą strategię jak pokazano w tym artykule stosujemy na co dzień pracując z modelami naszych klientów.
W modelowaniu numerycznym ważne jest przede wszystkim jasne określenie celu symulacji i odrzucenie tych elementów czy zjawisk, które niepotrzebnie komplikować będą zadanie (tutaj – ruchoma siatka). Po drugie, do rozwiązania dochodzimy stopniowo, od najprostszego modelu po skomplikowane, mocno nieliniowe układy (prosta siatka -> gęsta siatka, stały warunek brzegowy -> charakterystyka itp.). Dzięki takiemu podejściu jesteśmy w stanie dużo lepiej poznać fizykę zagadnienia oraz łatwo wskazać i naprawić błędy modelowe.
Na koniec polecam obejrzeć film w serwisie YouTube który zainspirował mnie do napisania tego artykułu:
Autor: Maciej Kryś
